每天一点统计学-二项分布公式的推导和使用

在《每天一点统计学——随机变量与概率分布》中已经初步了解了二项分布的基本概念和性质：

一次试验有且仅有两种可能结果：“成功”和“失败”，两个结果是随机决定且互斥的。

每次试验中，成功的概率是P，失败的概率是1-P，并且成功和失败的概率是常数或近似于不变

各次试验之间相互独立，每次试验结果不受其它各次试验结果的影响。

下面以高考一道数学单选选择题作为例子，完成二项分布公式的推导，也希望借此能够告诉大家在生活中如何使用二项分布。

数学知识都忘得差不多了，在这里我们也并不是要得出正确答案，但我们可以知道的几个事实是：

每道选择题都只有一个正确答案，其他三个为错误答案，每道题做题的结果只有正确和错误两种；

每道题做对的概率为0.25，做错的概率为0.75，它们的概率只和为1；

每道题相互独立、互不影响。

这就是一个二项分布的实际生活问题，先用概率树画出做题结果的分布情况：

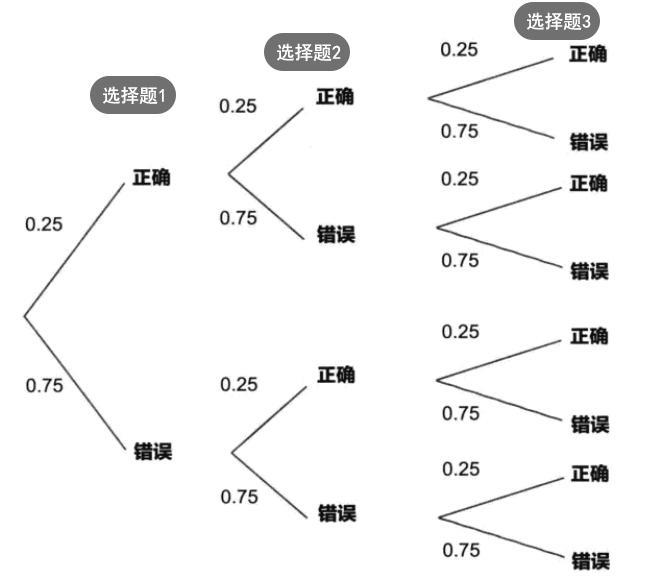
概率树

通过《每天一点统计学——排列与组合》中学到的知识，我们很容易得出下面的结果：

其中X表示总题数，r表示做对的题数，P（X=r）表示在总题数X中做对r道题数的概率

在三道选择题中做对r道题，这其实是一个组合问题，从P（X=r）中是不是发现了什么规律了呢？

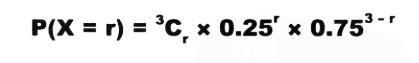
3道题中做对r道题的概率计算公式

二项分布公式

假设每道题的答对概率是p，而每道题答错概率是1-p，也就是q。而答对n个问题中的r个问题的概率为：

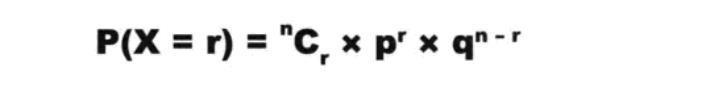
二项分布公式

回顾一下组合的计算公式：

组合

二项分布的期望和方差

再顺便提及以下二项分布期望和方差的计算公式，方差可以代表数据的变异性，而期望可以对决策做出指导作用：